Using Software Transactional Memory with the Dining Philosophers Problem

The Dining Philosophers Problem is a toy example used to demonstrate how deadlocks can occur in concurrent algorithms. In this problem, there are five philosophers sitting at a circular table, with five bowls of food and five chopsticks — one between each bowl.

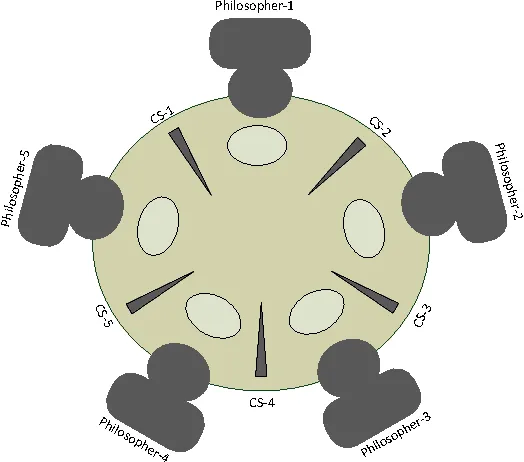
Each philosopher needs two chopsticks to eat from their bowl, and each philosopher needs to eat otherwise they will die of starvation. Instead of eating, a philosopher may also take time to think. Philosophers should eat concurrently, otherwise they may starve waiting for all the others to eat first. In the real world, the chopsticks represent a shared resource between processes (the philosophers).

A naive approach to this problem is to have each philosopher first reach for the left chopstick, then the right chopstick, and then eat. The problem with this is that each philosopher will indefinitely wait for the philosopher to their right to put down their chopstick. Since there is a circular dependency, this will never happen and all philosophers will starve to death. There are many solutions to this problem, such as asymmetric chopstick selection, limiting how many philosophers may eat at a time, etc. In this article, we will explore how Software Transactional Memory can be used to solve this problem.

Software Transactional Memory

Typically, programming with shared resources uses mutxes and semaphores to ensure exclusive access. These constructs, however, can be tedious to utilize correctly. For example, if one forgets to signal to a semaphore or even signals at the wrong time, a deadlock or some other synchronization conflict may arise. Software Transactional Memory (STM) acts as an abstraction layer to these constructs, so that the programmer can easily write concurrent algorithms without actually using these constructs.

This is done by allowing the programmer to create transactions which consist of a series of operations that are all guaranteed to run atomically as a whole. For instance, one could define a transaction that reads a value from a shared resource, applies an operation, and writes the new value to that shared resource, and not worry about any potential data races because all three operations are guaranteed to run atomically. In Haskell, this example might look like:

import Control.Concurrent.STM

incrementValue :: TVar Int -> STM () 
incrementValue ref = do 
  value <- readTVar ref 
  writeTVar ref (value + 1)

In the code above, TVar Int represents the shared Int resource to be incremented, and STM () represents that the incrementValue function is a monadic action. The STM monad is what allows the programmer to define transactions. It is important that this is completely separate from the IO monad, as arbitrary IO actions can violate the guarantees STM provides. This is also the reason why STM isn’t more widely used in languages like C or Java. These languages lack the ability to enforce this kind of separation.

In the Dining Philosophers Problem, the main issue was that Philosophers were grabbing one chopstick at a time, preventing any one philosopher to get two chopsticks to eat their food. Using STM, we can define a transaction that grabs both chopsticks atomically:

-- A Chopstick is a transactional semaphore
type Chopstick = TSem

data Philosopher 
    = Philosopher { leftStick  :: Chopstick
                  , rightStick :: Chopstick
                  }

grabChopsticks :: Philosopher -> STM ()
grabChopsticks p = do 
  waitTSem (leftStick p)
  waitTSem (rightStick p)

If a philosopher uses this transaction to try to grab two chopsticks and fails, then the transaction will retry (without busy waiting) until it is able to grab both. After this, we can define another transaction that sets both chopsticks down:

placeChopsticks :: Philosopher -> STM () 
placeChopsticks p = do 
  signalTSem (leftStick p)
  signalTSem (rightStick p)

And these two transactions can be used with the atomically function:

runPhilosopher :: Philosopher -> IO ()
runPhilosopher p = do 
  atomically (grapChopsticks p)
  -- ... eat food ...
  atomically (placeChopsticks p)

Even though there are no mutexes or semaphores (except for the Chopstick type synonym which is used only to make a smaller example), no deadlock can occur due to the mechanisms of STM.